Algoritma Tasarımı ve Analizi III (Algorithm Design and Analysis III)

Verinin hafızada sıralı tutulması için geliştirilen sıralama algoritmalarından biridir. Yığınlama sıralaması, arka planda bir yığın ağacı(heap) oluşturur ve bu ağacın en üstündeki sayıyı alarak sıralama işlemi yapar. Bu verilerin bir oluşumun belirleyici alanları olduğunu düşünebiliriz.

Algoritmanın Çalışması

Algoritma adımları şu şekilde özetlenebilir:

1. Sayı dizisinden bir ağaç oluşturulur.

2. Bu ağaç yaprak olmayan en son elemandan ilk(kök) elemana doğru heapify metoduyla yığınlaştırılır.

3. En üstte(kökte) duran yani en büyük olan değer alınarak sonuç dizisinin son elemanı yapılır.

4. Sonra geriye kalan sayılar tekrar yığınlaştırılır (heapify) ve bu işlem eleman kalmayana kadar yapılırsa sonuç dizisindeki veriler sıralanmış olarak elde edilir.

5. Bu sayı dizisi ilk başta verilen sayı dizisinin küçükten büyüğe sıralanmış halidir.

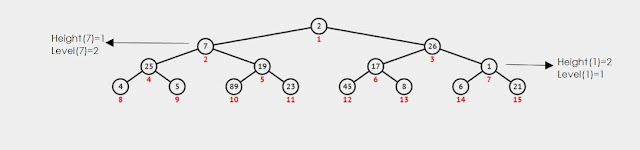
Düğüm Yüksekliği (Height of a Node): Düğümden itibaren düğümün yapraklara(leafs) uzaklığıdır.

Düğüm Seviyesi (Level of a Node): Düğümün köke(root) olan uzaklığıdır.

Ağaç Yüksekliği (Height of Tree): Kökün maksimum seviyedeki yaprağa olan uzaklığıdır.

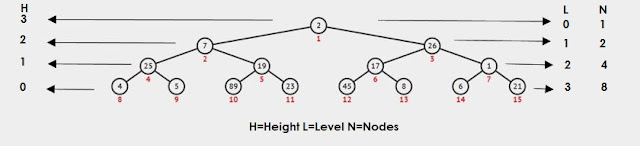
1. Her bir seviyedeki maksimum düğüm sayısı.

2. Ağaçta bulunması gereken maksimum düğüm sayısı.
3. n kadar düğümü olan ağacın yüksekliği.

$1. \: \: \: 2^{i}$

$2. \: \: \: \sum_{i=0}^{h}2^{i}=\frac{2^{h+1}}{2-1}=2^{h+1} -1$

$3. \: \: \: \left \lfloor lgn \right \rfloor$

Root: A[1]

Left child: A[i] = A[2i]

Right child: A[i] = A[2i + 1]

Parent: A[i] = A[ ëi/2û ]

HeapSize[A] ≤ length[A]

Max Heap (root en büyük eleman):

A[PARENT(i)] ≥ A[i]

Min Heap (root en küçük eleman):

A[PARENT(i)] ≤ A[i]

Max-Heap'e göre düzenlemek için: MAX-HEAPIFY
Heapify(Yığınlaştır) en büyük çocuğu, ebeveyni ile karşılaştırılır. Ebeveyn büyükse zaten heapify gereklerini sağlar, aksi durumda ise büyük çocuk ile ebeveyn yer değiştirir. Böylece ebeveyn kendi çocuklarından daha büyük olur.

public static void MaxHeapify( int[ ] arr, int i )
{
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int largest = i;

    if( left < arr.length && arr[ left ] > arr[ largest ] )
        largest = left;
    if( right < arr.length && arr[ right ] > arr[ largest ] )
        largest = right;
    if( largest != i )
    {
        int temp = arr[ i ];
        arr[ i ] = arr[ largest ];
        arr[ largest ] = temp;
        MaxHeapify( arr, largest );
    }
}

Sırasız bir diziden max-heap oluşturmak için: BUILD-MAX-HEAP

Bir diziyi A [ 1,…,n] dönüştürmek için aşağıdan yukarıya doğru Heapify fonksiyonu işletilir. Heap alt dizinin A [ n / 2 +1,…,n ] BUILD-HEAP ile alt dizi indisleri Heapfiy ile ağacın ebeveyn ve çocukları üzerinde swap(değiştirme) işlemi uygulanır.

public static void BuildMaxHeap( int[ ] arr )
{
    for( int i = (int)Math.floor(arr.length/2);i >= 0; i--)
        MaxHeapify( arr, i );
}

Diziyi sıralamak için: HEAPSORT

Yığın sıralama algoritması giriş dizisi A[1,…,n] üzerinde bir yığın oluşturmak için BUILD-HEAP fonksiyonu ile başlatılır. Kök A [1] bulunan maksimum eleman dizinin sonuna alınır ve dizi boyutu her döngüde bir azaltılır.

public static void HeapSort(int[ ] arr )
{
    int heapSize=arr.length;
    BuildMaxHeap(arr);
    for( int i = heapSize;i >= 0; i=i-2)
    {
        int temp = arr[ i ];
        arr[ i ] = arr[ 1 ];
        arr[ 1 ] = temp;
        heapSize=heapSize-1;
        MaxHeapify( arr, 1 );
    }
}

Heapify simülasyonu için kullanılacak sırasız dizi: A[2,7,26,25,19,17,1,90,3,36]

Level I

Level II

Level III

Level IV

Level V

Level VI

Level VII

Level VIII

Heapify simülasyonu için kullanılan dizinin sıralı yığınlaştırılmış hali: A[90,36,26,25,19,17,1,7,3,2]

MAX-HEAPIFY Çalışma Zamanı (Running Time)

Her seviye 2 karşılaştırma içerdiğinden 2h olur.

$O(2h)=0(h)=O(lgn)\: \: \: \: h=lgn$

MAX-HEAPIFY çalışma zamanı: O(lgn)

BUILD-MAX-HEAP Çalışma Zamanı (Running Time)
MAX-HEAPIFY BUILD-MAX-HEAP fonksiyonu içerisinde 1-n/2 aralığında döngü oluşturur.

$O(n/2)=0(n)$