Algoritma Tasarımı ve Analizi IV (Algorithm Design and Analysis IV)

Veriler Ne Kadar Hızlı Sıralanabilir ? 
Insertion sort, quick sort, heap sort ve merge sort gibi çoğu sıralama algoritmaları karşılaştırma yoluyla sıralama yapıyor. Karşılaştırma yaparak sıralama yapan uygulamaların en kötü durum çalışma süresi O(nlgn)'dir.  Bu çalışma süresi bu tür sıralama algoritmaları için çok yüksek bu nedenle Counting Sort algoritması ile bu çalışma süresini O(n) gibi düşük bir değer yapalım.

Sayarak Sıralama (Counting Sort)

Verinin hafızada sıralı tutulması için geliştirilen sıralama algoritmalarından birisidir. Basitçe sıralanacak olan dizideki her sayının kaç tane olduğunu farklı bir dizide saklar ve daha sonra bu sayıların bulunduğu dizinin üzerinde bir işlemle sıralanmış olan diziyi elde eder.

Bir karar ağacı ile karşılaştırma modeli elde edilebilir:

• Her n giriş boyutu için bir ağaç oluşturulur.

• Ağaç tüm olası durumlarda karşılaştırmalar içerir .

• Algoritmanın çalışma süresi = Alınan yolunun uzunluğu.

• En kötü durum çalışma süresi = Ağacın yüksekliği.

Teorem: . n elemanlı ve h yüksekliğindeki bir karar ağacını Ω(nlgn) çalışma süresinde sıralanabilir.

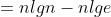
for i ← 1 to k do
    c[i] ← 0
for j ← 1 to n do
    c[A[j]] ← c[A[j]] + 1
//c[i] now contains the number of elements equal to i
for i ← 2 to k do
    c[i] ← c[i] + c[i-1]
// c[i] now contains the number of elements ≤ i
for j ← n downto 1 do
    B[c[A[i]]] ← A[j]
    c[A[i]] ← c[A[j]] - 1

Sayarak Sıralama Çalışma Zamanı (Counting Sort Running Time)

 1. 1-2 satırdaki döngü: O(k)

 2. 3-4 satırdaki döngü: O(n) 

 3.  6-7 satırdaki döngü: O(k) 

 4. 9-11 satırdaki döngü: O(n)

Genel Toplam: O(k) + O(n) + O(k) + O(n) = O(k + n)

Bu durumda çalışma süresi O(n) olur.

Level I

Level II

Level III

Level IV

Level V

Level VI

Level VII

Level VIII

Level IX

Level X

Level XI

Level XII

Level XIII

Level XIV 

Taban Sıralama (Radix Sort)

Bilgisayar bilimlerinde, tamsayı dizilerini artan ya da azalan bir şekilde sıralayabilecek birçok metot vardır. Radix Sort, sayıları basamaklarının üzerinde işlem yaparak sıralayan doğrusal sıralama algoritmalarından biridir. Radix Sort algoritması, 1887 yılında Hollerith’in patentini aldığı tabulating machine(tablolama makinesi) için kullandığı yönteme dayalıdır. Esasta, 2 tabanına göre yazılmış sayıları sıralayan hızlı bir algoritmadır. Sayma sayıları, adlar ya da tarihler gibi karakter dizilerini göstermek için de kullanılabildiğinden basamağa göre sıralama algoritması yalnızca sayma sayılarını sıralamak için kullanılan bir algoritma değildir. Radix Sort, hane sıralaması veya kök sıralaması isimleri ile de anılmaktadır.

Çoğu bilgisayar veri saklamak için ikilik tabandaki sayıların elektronikteki gösterim biçimlerini kullandığından sayma sayılarının basamaklarını ikilik tabandaki sayılardan oluşan öbekler biçiminde göstermek daha kolaydır. Basamağa göre sıralama algoritması,  en anlamsız basamağa göre sıralama ve en anlamlı basamağa göre sıralama olarak ikiye ayrılır. En anlamsız basamağa göre sıralama algoritması sayıları en anlamsız (en küçük, en sağdaki) basamaktan başlayıp en anlamlı basamağa doğru yürüyerek sıralarken en anlamlı basamağa göre sıralama algoritması bunun tam tersini uygular.

Taban Sıralama Çalışma Zamanı (Radix Sort Running Time)
0 – (k-1) Aralığında sayıları sıralamak için çalışma süresi Θ (n + k), b bit kelime r bitlik parçalar haline getirilirse, b/r parça için çalışma süresi Θ(n + 2r) olur.

Level I

Level II

Level III

Level IV

Level V

Level VI

Level VII

Level VIII

Level IX

Level X

Level XI

Level XII

Level XIII

Level XIV

Level V

Level VI

Bir sonraki yazımda görüşmek üzere...