Algoritma Tasarımı ve Analizi V (Algorithm Design and Analysis V)

Dinamik Programlama Nedir?

Dinamik programlama karışık problemlerin daha basit düzeylere indirilerek çözülmesini esas alan bir optimizasyon yöntemidir. Optimizasyondaki amaç, problemdeki kısıtlayıcı koşullar altında bu problemle ilgili en iyi kararı sağlamaktır. Bir problem üzerinde dinamik programlama uygulayabilmek için o problemin alt problemlere parçalanabilir veya bir önceki problemin karakteristiğini koruyacak şekilde çözümü daha kolay başka probleme dönüştürülebilir olması yeterlidir

Yönteme göre optimum çözüm başlangıç durumundan bağımsız olarak diğer çözümler ile çözüm sonuçlarına göre optimum çözümlerin ardışık olmasıdır. Yani, başlangıçta alt problemlerin çözümü bulunup elde edilen verilerle daha büyük alt problemler çözüldüğünde problemin kendisi de çözülmüş olur.

Dinamik programlama, aynı çözümlü küçük problemlere parçalanabilen tüm problemler için uygulanabilir. Fakat kaba-kuvvet (brute-force) ile üssel (exponential) zamanda çözülebilen problemlerde gerçek değerini gösterir. En basitinden fibonacci dizisinin hesabı O(2ⁿ) zaman karmaşıklığına sahipken, dinamik programlama ile problem O(n) zamanda çözülebilmektedir.

Dinamik Programlama ile çözülebilecek bazı problemler:

1.     Çubuk Kesme Problemi (Rod Cutting Problem)

2.     Knapsack Problem

3.     Zincir Matris Çarpım Problemi (Matrix Chain Multiplication Problem)

4.     Assembly Line Scheduling Problem

5.     En Uzun Ortak Alt Dizi (Longest Common Subsequence(LCS))

Hatırlatma (Memoization)

İhtiyaç duyulan bir değerin sürekli olarak hesaplanması yerine bir kere hesaplanıp ihtiyaç duyulduğunda bu değerin yeniden kullanılmasına denir. Bir fonksiyonel programlama dili olan haskell dilinde memoization işlemi otomatik gerçekleştirilmektedir. Memorization ile karıştırılmaması gerekir. Bir anlamıyla da hatırlama denebilir.

Bir problem için dinamik programlama algoritması yapmak için aşağıdaki dört adım uygulanır:

1.     En iyi çözümün karakteristiğinin belirlenmesi

2.     En iyi çözümün özyinelemeli tanımı

3.     En iyi çözümün değerini top-down veya bottom-up yaklaşımdan birini kullanarak hesaplanması

4.     Hesaplanmış verileri kullanarak en iyi çözümü bul

Bu adımlardan ilk 3’ü dinamik programlamanın temelidir. Eğer optimal çözümün yalnızca değerine ihtiyaç olursa bu temel adımları kullanmak yeterli olacaktır.

Zincir Matris Çarpımı Problemi (Chain Matrix Multiplication Problem)
Zincir matris çarpım problemi belki de dinamik programlamanın en popüler örneğidir. Zincir matris çarpımı bir dizi çarpım işlemi gerçekleştirmek için uygun sonuç dizisinin belirlenmesi problemini kapsar. Sorunun bu genel mantığı kod optimizasyonu ve veritabanlarında derleyici sorgu optimizasyonu tasarımı için önemlidir. Matris çarpımı ilişkisel bir işlem değil, değişmeli bir işlemdir. 

Matris A, p satır ve q sütun, yani matris boyutu p × q  ve B,  q satır ve r sütun, yani matris boyutu q × r  olan bir matris olsun.  Sonuç matrisi C boyutları p × r  olan bir matris olacaktır. A ve B matrislerini çarpmak için gerek şart A'nın sütun sayısı, B'nin satır sayısına eşit olmalıdır. 

Matris çarpım işlemlerinde geçerli bir sonuca ulaşmak için parentezleme kullanılabilir. Ama, her parentezleme işlemi aynı sayıda matris  içermek zorunda değildir. Parentezleme işlemini anlamak için A₁ , A₂ , A₃ matrislerini varsayalım.

A₁ boyutu 10 × 100 
A₂ boyutu 100 × 5  

A₃ boyut 5 × 50 olmak üzere:

MultCost [(( A₁ A₂ ) A₃ )] = (10. 100. 5) + (10. 5. 50) = 7500 skaler çarpım.

MultCost [( A₁ ( A₂ A₃ ))] = (100. 5. 50) + (10. 100. 50) = 75000 skaler çarpım.

İlk parantezleme işlemi diğerine göre 10 kat daha hızlı olduğu örnekte görülüyor.


Aşağıdaki 6 matrisi zincir matris çarpım yoluyla dinamik programlamaya uygunluğu ve asimtotik notasyonunu bulalım.

       
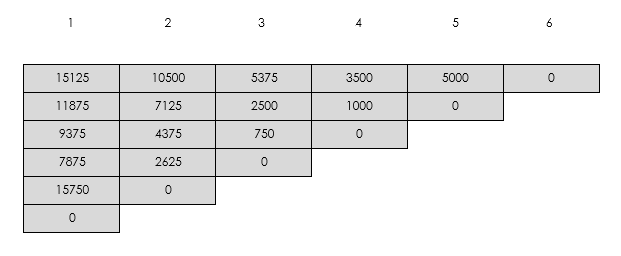
Matris çarpımı için formülde i ve j indislerinin eşit olduğu hücreler 0 olarak değerlendirilir.


                              

Level I

Bilinen hücrelerden bilinmeyen hücreleri bulmak için genel formülden hesaplanır. 

                                                                        

Level II

Eğer bir hücreye birden fazla k değeriyle yaklaşılırsa (k=1, k=2) bu değerlerden minimum değer hücreye alınır.


                  

Level III

                                 
Diğer hücrelerde aynı yolla doldurulur ve tüm hücreleri doldurabilme işlevi bu zincir matris işleminin dinamik programlamaya uygunluğunun tespitidir. 


                            
                           
                            

Level IV

Son hücre için k değerine n-1 değerine kadar hesaplanır ve minimum değer son hücrenin değerini belirler. 

       

Level V

Bu alanda ise son hücreye minimum maliyetle erişim için kullanılan hücreler işaretlenmiştir.

Level VI

Zincir Matris Çarpım Problemi .java kodu:

package MCM;

import java.io.*;
import java.util.*;
import java.lang.StringBuffer;

public class MCM {

    public int N[][];
    public int d[];
    public int SIZE = 5;

    public static void main(String[] args) throws Exception {
        MCM mcm = new MCM();

        mcm.init();

        // Matris çarpımında en son hücrenin minimum elemanı
        int result = mcm.minMCM();

        System.out.println("sonuc = " + result);
    }

    public void init() {
        N = new int[SIZE][SIZE];
        d = new int[SIZE + 1];

        // N matrisinin belirli alanları doldurulur. 999 olan alanlar bos
        for (int i = 0; i < SIZE; i++) {
            for (int j = 0; j < SIZE; j++) {
                if (i == j) {
                    N[i][j] = 0;
                } else {
                    N[i][j] = 999;
                }
            }
        }

        // 5 Matrisin satır ve sütun sayıları tanımlandı.
        d[0] = 1;
        d[1] = 4;
        d[2] = 2;
        d[3] = 3;
        d[4] = 1;
        d[5] = 4;
    }

    // bu metot minimum elemanı verir.
    public int minMCM() {

        for (int i = 1; i <= SIZE; i++) {
            for (int j = 0; j <= SIZE - i; j++) {
                for (int k = j; k < j + i - 1; k++) {
                    if (N[j][j + i - 1] > N[j][k] + N[k + 1][j + i - 1] + d[j] * d[k + 1] * d[i + j]) {
                        N[j][j + i - 1] = N[j][k] + N[k + 1][j + i - 1] + d[j] * d[k + 1] * d[i + j];
                    }
                }
            }
        }

        System.out.println("Matris N = ");
        for (int i = 0; i < SIZE; i++) {
            for (int j = 0; j < SIZE; j++) {
                if (N[i][j] == 999) {
                    System.out.print(" " + "\t");
                } else {
                    System.out.print(N[i][j] + "\t");
                }
            }
            System.out.println();
        }

        System.out.println();

        return N[0][SIZE - 1];
    }
}

Bir sonraki yazımda görüşmek üzere...