En
Kısa Yol Problemi (Shortest Paths Problem)
Ağ üzerinde bir düğüm ile diğer düğümler arasında
en kısa yolu bulmak için düğüm etiketleri kullanır. Her aşamada etiketlenmiş ve
etiketlenmemiş düğümler oluşacaktır. Düğümün etiketlenmesi seçilen düğüm ile
arasında seçilmiş bir yolun olduğunu gösterir. Etiketlenmemiş düğümlerde ise
böyle bir yol seçilmemiş demektir. Ayrıca etiketler sabit ve geçici etiket
olarak ikiye ayrılır. En kısa yol seçildiğinde düğümün etiketi sabit olur. Eğer
en kısa yol seçilmediyse düğümün etiketi geçici olur.
Negatif kenar ağırlıkları:
1. Negatif ağırlıklı döngü olmadığı zaman sorun olmayacaktır.
2. Negatif ağırlığa sahip döngü varsa, sürekli bu döngü hareket ederek yol kısaltılabilir.
Negatif kenar ağırlıkları:
1. Negatif ağırlıklı döngü olmadığı zaman sorun olmayacaktır.
2. Negatif ağırlığa sahip döngü varsa, sürekli bu döngü hareket ederek yol kısaltılabilir.
En
Kısa Yol Problemi Uygulamaları (Shortest Paths Problem Applications)
1. PERT / CPM
2. Harita yönlendirme
3. Doku haritalama
4. Robot navigasyon
6. Kentsel trafik planlaması
7. VLSI yonga optimal pipelining
8. Telemarketer operatörü zamanlama
9. Telekomünikasyon mesajlarının yönlendirme
10. Ağ yönlendirme protokolleri (OSPF, BGP, RIP)
11. Döviz arbitraj fırsatları kullanma
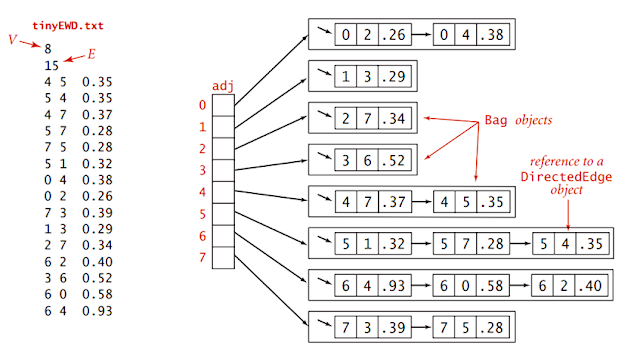
Hedef: Her düğüme olan kısa yolu bulun.
distTo
[V] s 'den v'ye en kısa yolun uzunluğudur.
edgeTo
[V] s, v kısa yoldan
geçilen düğümdür.
Kenar
Gevşetme (Edge Relaxation)
Relax edge e = v→w.
1. distTo[W] s w arasındaki en kısa yolu bilinen
uzunluğudur.
2. edgeTo[W]
s w kısa bilinen yolda son kenarıdır.
3. e = v → w v aracılığıyla w kısa yolunu verirse,
hem distTo[W] ve edgeTo[W] güncellenir.

En
Kısa Yol Optimallik Koşulları
G bir kenar ağırlıklı digraph alalım.
Sonra distTo[] s için en kısa yol mesafeleri
şunlardır:
1. distTo [S] = 0.
2. Her bir köşe için distTo [V] s, v arasındaki en kısa yolun uzunluğudur.
3. e = v→w her kenar için distTo[W] ≤ distTo [V] +
e.weight [W] olmalıdır.

s,w’ye en kısa yollar: s = v0 → v1 → v2 → … → vk =
w
distTo[v1] ≤ distTo[v0] + e1.weight()
distTo[v2] ≤ distTo[v1] + e2.weight()
...
distTo[vk] ≤ distTo[vk-1] + ek.weight()
Bu eşitsizlikler sadeleştirilirse:
distTo[w] = distTo[vk] ≤ e1.weight() + e2.weight()
+ … + ek.weight()
Hangi algoritma en kısa yol probleminde kenar
gevşetme için seçilir?
1. Dijkstra Algoritması (negatif olmayan
ağırlıklar)
2. Bellman-Ford Algoritması (negatif döngüler)
Dijkstra
Algoritması (Dijkstra Algorithm)
Dijkstra Algoritması en kısa yol hesaplarında en çok kullanılan yöntemlerdendir. Bilgisayar ağları, taşımacılık, posta gibi hizmetlerde bir çok gerçek uygulamada kullanılmaktadır. Belki de en önemli uygulaması İnternet’in temel yönlendirme algoritması olan OSPF (Open ShortestPathFirst) için bir temel oluşturmasıdır. Bu algoritma yönlendirilmiş ve yönlendirilmemiş çizgeler için kullanılabilir.
Çizgenin pozitif değerlerle ağırlıklandırılmış olması zorunludur (negatif kenar ağırlığı bulunamaz).
Bu algoritma da açgözlü problem çözme yaklaşımını takip eder, verilen bir başlangıç düğümünün önce komşularına olan en kısa yolu bulur, daha sonra onların komşularına, ve aynı şekilde çizge içindeki tüm düğümlere olan en kısa yolları bulmuş olur.
Dijkstra Algoritması en kısa yol hesaplarında en çok kullanılan yöntemlerdendir. Bilgisayar ağları, taşımacılık, posta gibi hizmetlerde bir çok gerçek uygulamada kullanılmaktadır. Belki de en önemli uygulaması İnternet’in temel yönlendirme algoritması olan OSPF (Open ShortestPathFirst) için bir temel oluşturmasıdır. Bu algoritma yönlendirilmiş ve yönlendirilmemiş çizgeler için kullanılabilir.
Çizgenin pozitif değerlerle ağırlıklandırılmış olması zorunludur (negatif kenar ağırlığı bulunamaz).
Bu algoritma da açgözlü problem çözme yaklaşımını takip eder, verilen bir başlangıç düğümünün önce komşularına olan en kısa yolu bulur, daha sonra onların komşularına, ve aynı şekilde çizge içindeki tüm düğümlere olan en kısa yolları bulmuş olur.
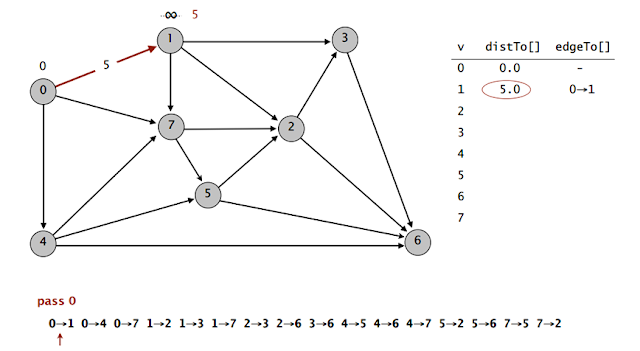
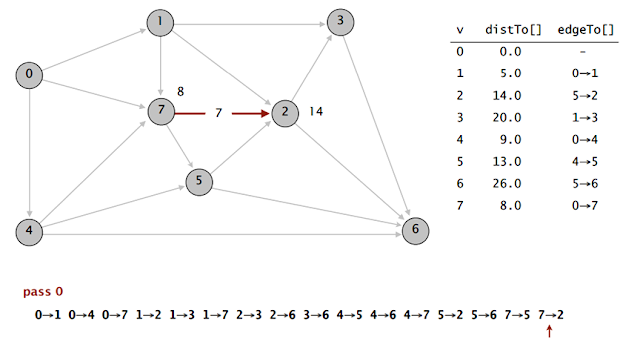
Aşağıdaki grafın optimal en kısayol çözümü yapılmıştır.


Bellman-Ford
Algoritması (Bellman-Ford Algorithm)
Bellman-Ford algoritmasının amacı, bir graf üzerindeki,
bir kaynaktan bir hedefe giden en kısa yolu bulmaktır. Bu anlamda en kısa yol
bulma algoritması olarak sınıflandırılabilir. Algoritma ağırlıklı graflar
üzerinde çalışır. Bütün düğümler için bütün kenarları dolaşır. Dolayısıyla
performansı düğüm sayı ile kenar sayısının çarpımı olarak düşünülebilir. O(V.E)
Algoritmasında iç içe iki döngü, kenar ve düğüm
sayısı kadar dönmektedir. Ayrıca, bir düğümdeki değerin güncellenmesi
sırasında, hangi düğümden gelindiği bilgisi de tutulmaktadır. Bu durum eksi
yüklü kenarlar için çözüm oluşturur. Örneğin Dijkstra algoritmasında olan ve
negatif değerli kenarlardan kaynaklanan döngüye girilme ihtimali, Bellman-Ford
algoritmasında bulunmaz.
Algoritma Dijkstra algoritmasında olduğu gibi en
küçük değere sahip olan kenardan gitmek yerine tüm graf üzerindeki kenarları
test ederek dolaşır. Bu sayede aç gözlü yaklaşımını (greedy approach)
kullanmaz ve her düğüme sadece bir kere bakarak en kısa yolu bulmuş olur.
 |
| Level I |
 |
| Level II |
 |
| Level III |
 |
| Level IV |
 |
| Level V |
 |
| Level VI |
 |
| Level VII |
 |
| Level VIII |
 |
| Level IX |
 |
| Level X |
 |
| Level XI |
 |
| Level XII |
 |
| Level XIII |
 |
| Level XIV |
 |
| Level XV |
 |
| Level XVI |
 |
| Level XVII |
 |
| Level XVIII |
 |
| Level XIX |
 |
| Level XX |
 |
| Level XXI |
 |
| Level XXII |
 |
| Level XXIII |
 |
| Level XXIV |
 |
| Level XXV |
 |
| Level XXVI |
 |
| Level XXVII |
 |
| Level XXVIII |
Bir sonraki yazımda görüşmek üzere...